Basic Amplifier Configurations

Q1: What are the basic amplifier configurations? $\frac {g_mr_\pi R_E}{1+(\frac{R'_L}{r_o})(1+\frac{R_E}{r_\pi})}$
A1: There are 8 basic amplifier configurations: 4 basic BJT amplifier configurations and 4 basic MOS amplifier configurations. Note that that taking the limit as $r_\pi \to \infty$ of the BJT equations produces the MOS equations.

Common Base:

$A_v=g_m(r_o || R'_L)$

$R_i=r_\pi || \frac {r_o+R'_L}{1+g_mr_o}$ 

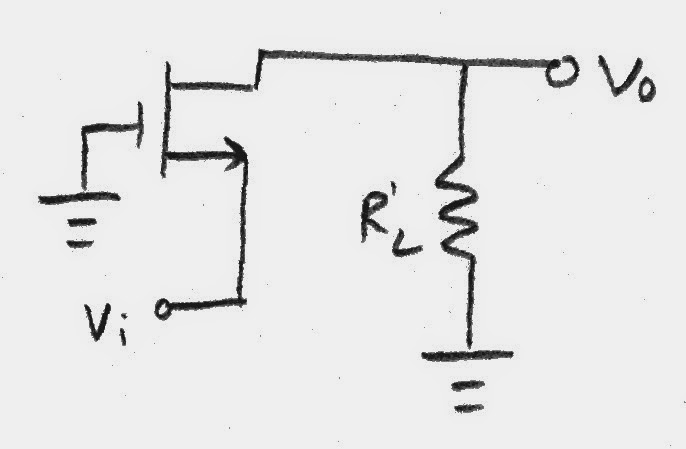Common Gate:

$A_v=g_m(r_o || R'_L)$

$R_i= \frac {r_o+R'_L}{1+g_mr_o}$  

Common Source:

$A_v=-g_m(r_o || R'_L)$

$R_i=\infty$ 

Common Emitter:
$A_v=-g_m(r_o || R'_L)$
$R_i=r_\pi$ 

Common Emitter with $R_E$:

$A_v=-\frac{g_mR'_L}{1+g_mR_E+(R'_L/r_o)(1+R_E/r_\pi)}$

$R_i=r_\pi + \frac {g_mr_\pi R_E}{1+(R'_L/r_o)(1+R_E/r_\pi)}$

Common Source with $R_S$:

$A_v=-\frac{g_mR'_L}{1+g_mR_E+(R'_L/r_o)}$

$R_i=\infty$

Common Collector/Emitter Follower:

$A_v=\frac{g_m(r_o || R'_L)}{1+g_m(r_o || R'_L)}$

$R_i=r_\pi + \beta (r_o || R'_L)$ 

Common Drain/Source Follower:

$A_v=\frac{g_m(r_o || R'_L)}{1+g_m(r_o || R'_L)}$

$R_i=\infty$ 

Introduction to Small Signal Model

Q1: How can I analyze real amplifier circuits?
A1: You can divide the amplifier circuit into its signal circuit and bias circuit. For now, we will consider the signal circuit.

Q2: How do I map real circuit elements to their signal circuit counterparts?
A2: By using their small signal models (SSM):

Resistors and capacitors behave the same in signal circuits

Independent voltage sources mapped to short circuits while
independent current sources are mapped to open circuits

Things change a bit with nonlinear elements.
The diode maps to a resistor of $r_d=\frac{nV_T}{I_D}$

$r_\pi=\frac{V_T}{I_B}$
$g_m=\frac{I_C}{V_T}=\frac{\beta}{r_\pi}$
$r_o\approx \frac{V_A}{I_C}$

Both the NPN and PNP map to the same SSM

$g_m=\frac{2I_D}{V_{OV}}$
$r_o\approx \frac{1}{\lambda I_D}$
Both the NMOS and PMO map to the same SSM

Mirror Circuit

Q1: What's a mirror circuit?
A1:

$Q_{ref}$ and $Q_1$ are identical NPN transistors.
This is why current splits evenly to each of their bases.

Q2: What state is $Q_{ref}$ in?
A2: Since $i_{C,ref}>0$, we know that $Q_1$ must be on. Hence, $V_{BE,ref}=V_{D0}$
Note that the base and collector share the same node in $Q_{ref}$.
Hence, $V_{BE,ref}=V_{CE,ref}=VD_{0}$
Therefore, $Q_{ref}$ is always active.

Q3: How is $I_1$ related to $I_{ref}$?
A3: First, let's find an expression for $I_{ref}$:
By KCL: $I_{ref}=2i_B+i_{c,ref}$
Since $Q_{ref}$ active: $I_{ref}=2\frac{i_{C,ref}}{\beta}+i_{C,ref}$
$I_{ref}=i_{C,ref}(\frac{2}{\beta}+1)$

Next, let's examine $I_1$:
$I_1$=$i_C$
$I_1=\beta i_B$
$I_1=\beta \frac{i_{C,ref}}{\beta}$
$I_1=i_{C,ref}$
$I_1=\frac {I_{ref}}{\frac{2}{\beta}+1}$

For $\beta \gg 1$:
$I_1\approx I_{ref}$

By KVL through $Q_{ref}$ (either the BE or CE branch):
$I_1\approx I_{ref}=\frac{V_{CC}-V{D0}+V{EE}}{R}$

Q2: Why use a mirror circuit?
A2: You can use a mirror circuit to behave as a current source in order to bias a BJT.

Q3: Why not use a mirror circuit?
A3: The mirror circuit produces integer multiples of the reference current. For a more flexible option, you might want to look into current-steering circuits.

MOS Circuits

Q1: What states can a MOS be in?
A1: A NMOS may be in:

1. Cutoff
• $v_{OV}\leq 0$
• $i_D=0$
2. Saturation
• $v_{OV}\geq 0$ and $v_{DS}\geq v_{OV}$
• $i_D=0.5\mu_nC_{ox}\frac{W}{L}v_{OV}^2(1+\lambda v_{DS})$
3. Triode
• $v_{OV}\geq 0$ and $v_{DS}\leq v_{OV}$
• $i_D=0.5\mu_nC_{ox}\frac{W}{L}(2v_{OV}v_{DS}- v_{DS}^2)$

A couple of notes:

• $v_{OV}=v_{GS}-v_{tn}$ where $v_{OV}$ is the overdrive voltage and $v_{tn}$ is the threshold voltage associated with the NMOS
• The expressions for $i_D$ in saturation and triode both contain the pre-factor $0.5\mu_nC_{ox}\frac{W}{L}$ 
• $\mu_n$ is the negative charge carrier effective mobility
• $C_{ox}$ is gate-oxide capacitance per unit area
• $W$ is the gate width
• $L$ is the gate length
• The expression for $i_D$ in saturation contains the channel-length modulation parameter $\lambda$. 
• If channel-length modulation can be neglected, then $\lambda=0$
• The channel-length modulation parameter is related to early voltage by: $\lambda=\frac{1}{v_A}$
• The phenomenon of channel-length modulation in MOSFETs can be compared to Early effect in BJTs

For a PMOS:

1. $v_{OV}=v_{GS}-v_{tn}\to v_{OV}=v_{SG}-|v_{tp}|$
2. $\mu_n \to \mu_p$
3. $v_{DS}\to v_{SD}$
4. $v_{GS}\to v_{SG}$

Q2: How do I solve MOS circuits?

A2: For an NMOS circuit:

1. Write the KVLs for $v_{GS}$ and $v_{DS}$
2. Assume cutoff by setting $i_D$=0. Check that you are in cutoff.
3. Assume saturation. Check that $v_{DS}\geq v_{OV}$
4. You're in triode mode. 

Note that the equations for $i_D$ in saturation and triode mode are quadratic. Although you may find 2 roots, only keep the 1 that's valid for that particular state.

MOS Device

Q1: What is a MOSFET?
A1: A MOSFET is a metal oxide semiconductor field-effect transistor. They're often abbreviated as MOS devices. A MOSFET has 4 terminals:

1. Gate
2. Body
3. Drain
4. Source

Q2: What are some types of MOS devices?

A2: There's n-channel metal oxide semiconductor (NMOS) and p-channel metal oxide semiconductor (PMOS).

Current direction is reversed in the PMOS

Note the 4 terminals of the NMOS

In practice, the body terminal is often connected
to the source terminal of the NMOS

Same goes for the PMOS

Combining the body and source terminals
simplifies the NMOS to a 3 terminal device

Same for the PMOS

Q3: What circuit variables do I need to look for in a MOSFET?
A3: For a MOSFET in which the body and source terminals are connected, there are only 3 currents and 3 voltages to deal with. By KVL, you know that 1 voltage may be written in terms of the other 2. Same goes for current. So it looks like we need to account for 4 circuit variables, as was the case for the BJTs. However, MOSFETs differ from BJTs in that one current is already specified: $i_G$ is always 0. Hence, you only need to keep track of 3 circuit variables.

For an NMOS you might choose to keep track of:

1. $i_D$
2. $v_{GS}$
3. $v_{DS}$

For a PMOS, the current direction is reversed and the voltage subscripts are flipped. 

Universal and Empty Set

Q1: What is the complement of a set $A$?
A1: The complement of a set $A$ is the set that contains all elements that do not belong to A.

$A^c=\{ x: x\not\in A\}$

It follows that:
$(A^c)^c=A$

Q2: What is the universal set?
A2: The universal set $\Omega$ is the set that contains all conceivable elements.
Hence, $A \cup A^c = \Omega$

Q3: What is the complement of the universal set?
A3: The empty set {} is the complement of the universal set. The empty set contains no elements.
Hence, $A \cap A^c = \{\}$

Union and Intersection

Q1: What is a union of sets?
A1: A union of sets is a a set whose elements are belong to at least one of the sets in the union.
Given: For 2 sets $A$ and $B$:
$A\cup B=\{ x: x\in A\ or\ x\in B\}$
Given: For countable collection of infinite sets $C_1, C_2, C_3, ...$:
$\bigcup\limits_{i=1}^{\infty}C_i=C_1 \cup C_2 \cup C_3 \cup ... =\{ x: x\in C_i\ for\ some\ i\}$

Q2: What is an intersection of sets?
A2: An intersection of sets is a set that contains only those elements that are shared by all sets that form the intersection.
Given: For 2 sets $A$ and $B$:
$A\cap B=\{ x: x\in A\ and\ x\in B\}$
Given: For countable collection of infinite sets $C_1, C_2, C_3, ...$:
$\bigcap\limits_{i=1}^{\infty}C_i=C_1 \cap C_2 \cap C_3 \cap ... =\{ x: x\in C_i\ for\ all\ i\}$

Q3: What is a disjoint collection of infinite sets $C_1, C_2, C_3, ...$?
A3: A disjoint collection of infinite sets is a collection of sets whose intersection is the empty set.
$\bigcap\limits_{i=1}^{\infty}C_i=\{\}$

Q4: What does it mean if a family of sets $P$ composed of cells $P_1, P_2, P_3, ...$ partition a set $A$?
A5: If $P$ partitions a set $A$, the following 3 conditions hold:

1. The partition does not contain the empty set
• $\{\}\not\in P$
2. The union of the cells is the set $A$. The partition covers $A$.
• $\bigcup\limits_{i=1}^{\infty}P_i=A$
3. No 2 cells share any elements. The partition is pairwise disjoint.
• $P_i\cap P_j=\{\}\ for\ all\ i\not =j$